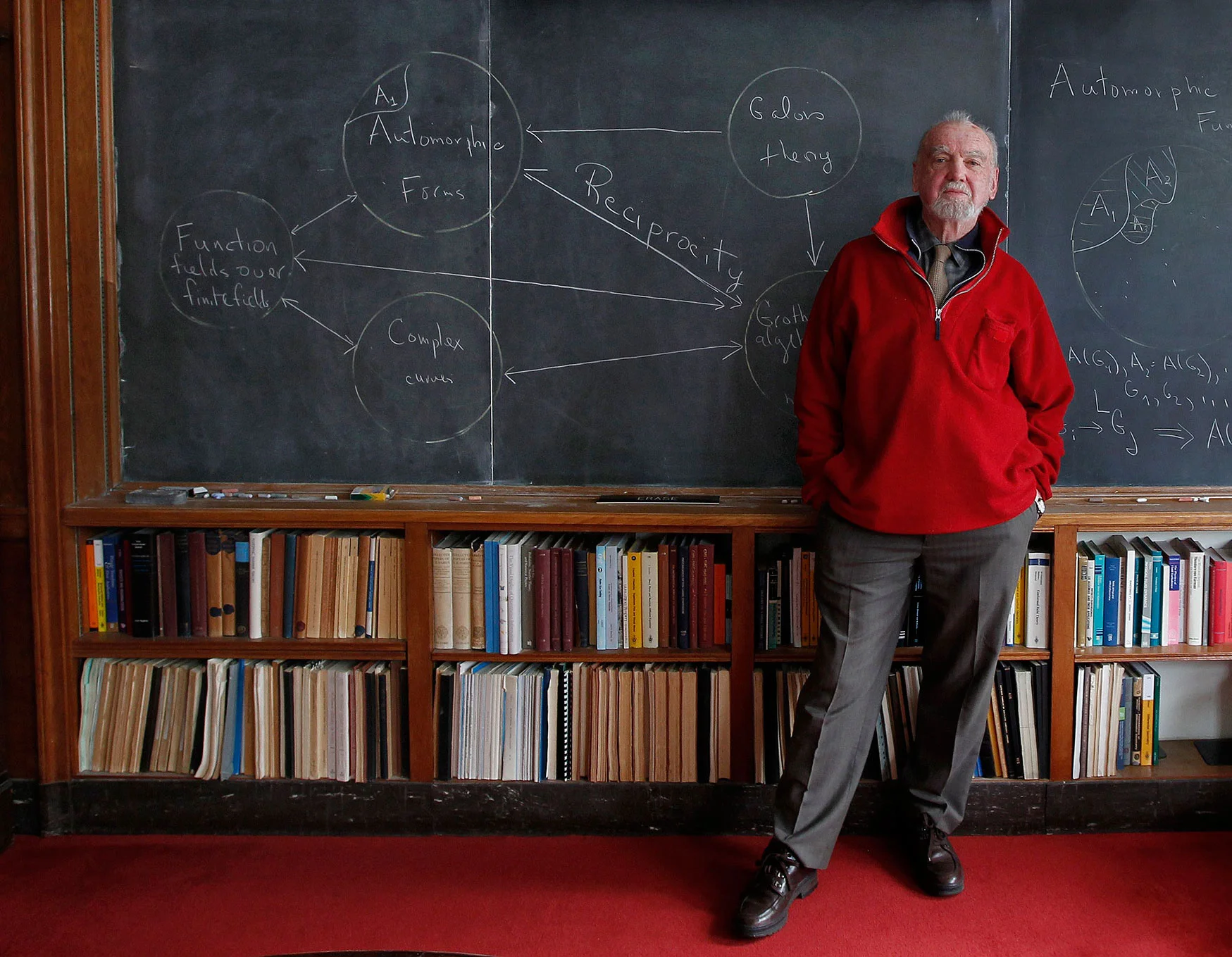
MEANING OF FEYNMAN DIAGRAMS | MICHAEL H SEYMOUR

School of Physics & Astronomy University of Manchester
& Theoretical Physics Group ( PH-TH ) CERN

|| ABSTRACT ||

Feynman diagrams are often used as a " cartoon " to explain the physics process being studied in a particular reaction .

However , they are also a summary of the mathematical calculation that needs to be made in order to predict the rate of that reaction .

In this set of three lectures , which were given at the CERN High School Teachers' Programme , I attempt to explain this mathematical basis of Feynman diagrams , without introducing many mathematical details .

I am very interested to receive comments and suggestions , both from experts and interested non-experts , on how this explanation can be improved .

|| INTRODUCTION ||

You will encounter Feynman diagrams in almost any popular discussion of particle physics , and certainly in several of the lecture courses of the High School Teachers' ( HST ) programme .

In most of these contexts , they are used in a rather cartoon-like way , to illustrate the physical process under
discussion .

However , mention is usually made of the fact that they mean much more than this — they are a summary of the precise mathematical ingredients that must be put together in order to calculate the properties of that process , in particular its rate .

In discussion with the teachers in previous years' HST programmes , it became clear that some of them were uncomfortable with this — they were nervous in using Feynman diagrams as cartoons , because they were hazy on the mathematical foundation that supposedly underlies them .

In these lectures I will attempt to bridge this gap , to present the meaning of Feynman diagrams .

It is a formidable task , essentially to present the complex mathematical basis of the whole of particle physics, called quantum field theory, without introducing any complex mathematics .

It is inevitable therefore that the mathematical level of these lectures is higher than most of the others in the HST programme .

I have tried to organize the material in a progressive order of complexity — the first lecture is mostly pictures and ideas , and at the end I will review some of the mathematics that I will need in the second lecture .

That will introduce the key equations , and the so-called " Feynman rules in x space " , and will show that the Feynman rules for scattering processes reproduce Coulomb's Law .

Finally in the third lecture , I will convert the Feynman rules to " momentum space " , the form in which they are always used in practice , discuss some subtleties related to antiparticles , and a more advanced application of the rules .

In the lectures themselves I merely state the relevant formulae and do not derive them .

I am aware that some people might find this unsatisfactory and attempt to give simple proofs of as many results as possible in the appendix . You are then free to study these at your leisure .

The approach is mostly that of Halzen and Martin , although the explanations are largely my own .

CLICK TO CONTINUE TO 16 PAGE PDF ➤➤

SOURCE | SATYAVEDISM.ORG